はじめに角錐・円錐の体積について解説していきます。 体積はどちらも 『体積=底面積×高さ×1 3 1 3 』 となります。 このときの "高さ" とは、 頂点から底面に下ろした垂線の長さ です。よって、小さな円錐の体積は、 $\pi b^2\times\dfrac{bh}{ab}\times\dfrac{1}{3}=\dfrac{\pi b^3h}{3(ab)}$ です。 一方、大きな円錐の高さは、 $xh=\dfrac{bh}{ab}\dfrac{(ab)h}{ab}=\dfrac{ah}{ab}$ となります。 したがって、大きな円錐の体積は、またまた「小中学生にもわかる」シリーズだが、 今回は「錐体の体積は底面積×高さ÷3」 という公式についてである。 この公式は小学校高学年で教わることになっているが、 子供に 「なんで÷3かわかる?」 と聞くと、

高校入試対策数学 円錐に関する対策問題 Pikuu
円錐の体積の公式証明
円錐の体積の公式証明-円錐の体積の公式は「πr 2 h/3」です。 円柱の体積の1/3の値が円錐の体積といえます。 また円錐だけでなく「錐体」の体積は、柱体の体積の1/3となるので覚えておきましょう。円錐 円すい 体積計算 公式 求め方 高さ 直径 自動 volume




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは、 「進研ゼミ円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm
円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.円柱 (えんちゅう) の体積 体積=πr2h 体積 = 半径 ×体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!
この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより円錐の体積が得られるのかを, 定積分法 と 区分求積法 を用いて説明する.円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。 これなら3秒で円錐の体積を計算でき立体の体積 角柱、円柱の体積 柱の体積 = 底面積 ×



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の体積の公式は、 V = 1 3 πhr2 V = 1 3 π h r 2 だから、高さ = 9 = 9 , 半径 = 5 = 5 を代入して、 V = 1 3 ×円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱積分計算による体積の求め方! 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通して



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
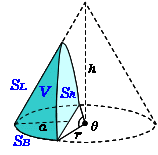



一部が欠けた直円錐の体積 高精度計算サイト
れた錐体の求積に関する指導のあり方を考究するものである。 柱体の体積や錐体の体積を考えるに当たり,児童にとっては その1つの考える道筋として面積からの対比や類比が考えられ る。さらに,このことをもとに体積に着目していくならば,と52 = 75π V = 1 3 ×三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。
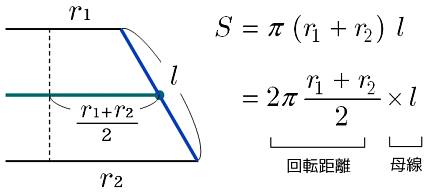



初等幾何 円錐台の側面積を求める 大人が学び直す数学




円錐の表面積の求め方 公式と計算例
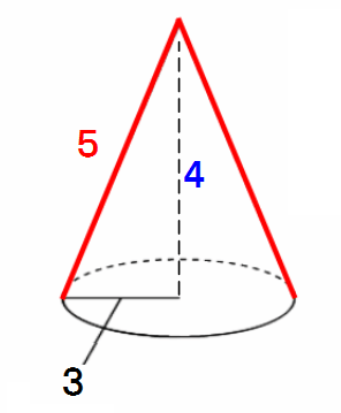
高さ 錐体の公式 錐 (すい) の体積は、底面積 S、高さ hとして、次の式で求められます この公式も、底面の形にかかわらず使えます。 錐体 (すいたい) の体積 体積=1/3Sh 体積 = 底面積 ×体積の公式は? 体積の公式は、柱体(ちゅうたい)、錐体(すいたい)、球(きゅう)で式が違います。特に、柱体と錐体の体積の公式はよく使うので覚えましょうね。下記に示します。 柱体(ちゅうたい) ⇒ 底面積×高さまとめ 円錐の高さを求める問題は、ほぼこの2パターン! 母線と半径から、三平方の定理を使って求める 体積と半径から、円錐の体積の公式を使って求める はかせちゃん 今日もお疲れ様でした~ また会える日を楽しみにしていますね 関連記事は
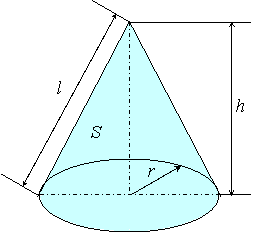



数学の公式集 No 012 幾何図形 円錐の体積と表面積



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com
回転体の体積を求めさせる問題の多くは回転軸が x x x 軸または y y y 軸です。しかし,たまに回転軸が斜めになっているものも出題されます。そのような斜回転体の求積に対応するための公式が傘型分割公式です。斜切円柱の体積 楕円柱の体積 直円錐の体積 斜切円錐の体積 一部が欠けた直円錐の体積 円錐台の体積 楕円錐の体積 楕円錐台の体積 球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積円錐台の体積の公式 S:はじめまして。いつもホームページ読ませていただいてます。 さて、円錐の体積で教えてほしいことがあります。 円錐を底面からhの高さで底面と水平にスパッと切った時の体積なのですが、真横からみると台形になる。
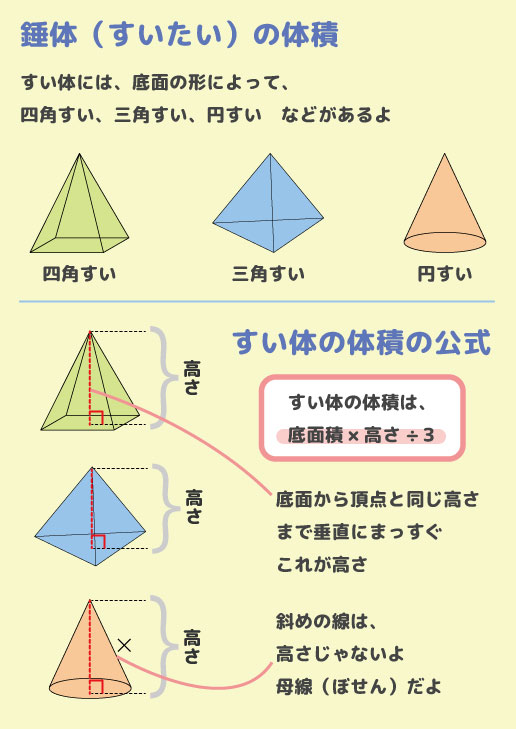



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強
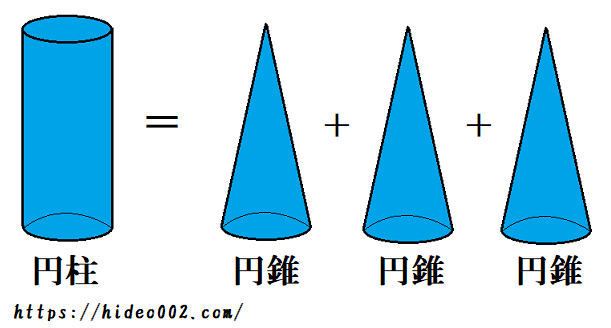



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋
前回 https//youtube/suE8iejgX7I 次回 https//youtube/E2uvg8kfcV4 数学検定 3級 268回 2次 5の過去問解説です。円錐台の体積を錐体の体積公式を知っているが積分計算は知らない場合(日本の多くの小中学生はそうである)、体積を求めるには、円錐から小円錐を取り除いたと考えればよい。円錐台の上底の半径を r 1, 下底の半径を r 2, 高さを h とすると、もとの大きな円錐の高さ H は角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高




積分を用いた円錐の体積公式の導出 頭の整理



円錐とは 体積 表面積の公式や求め方 受験辞典
5 2 = 75 π だね! はかせちゃん あっさりしすぎたかな お疲れ様でした~ 関連記事はこちら 中学数学円錐の表面積円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学
円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体錐体(円錐、角錐)の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




球の表面積と体積の公式 数学fun



円錐 体積の比較 中学から数学だいすき




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
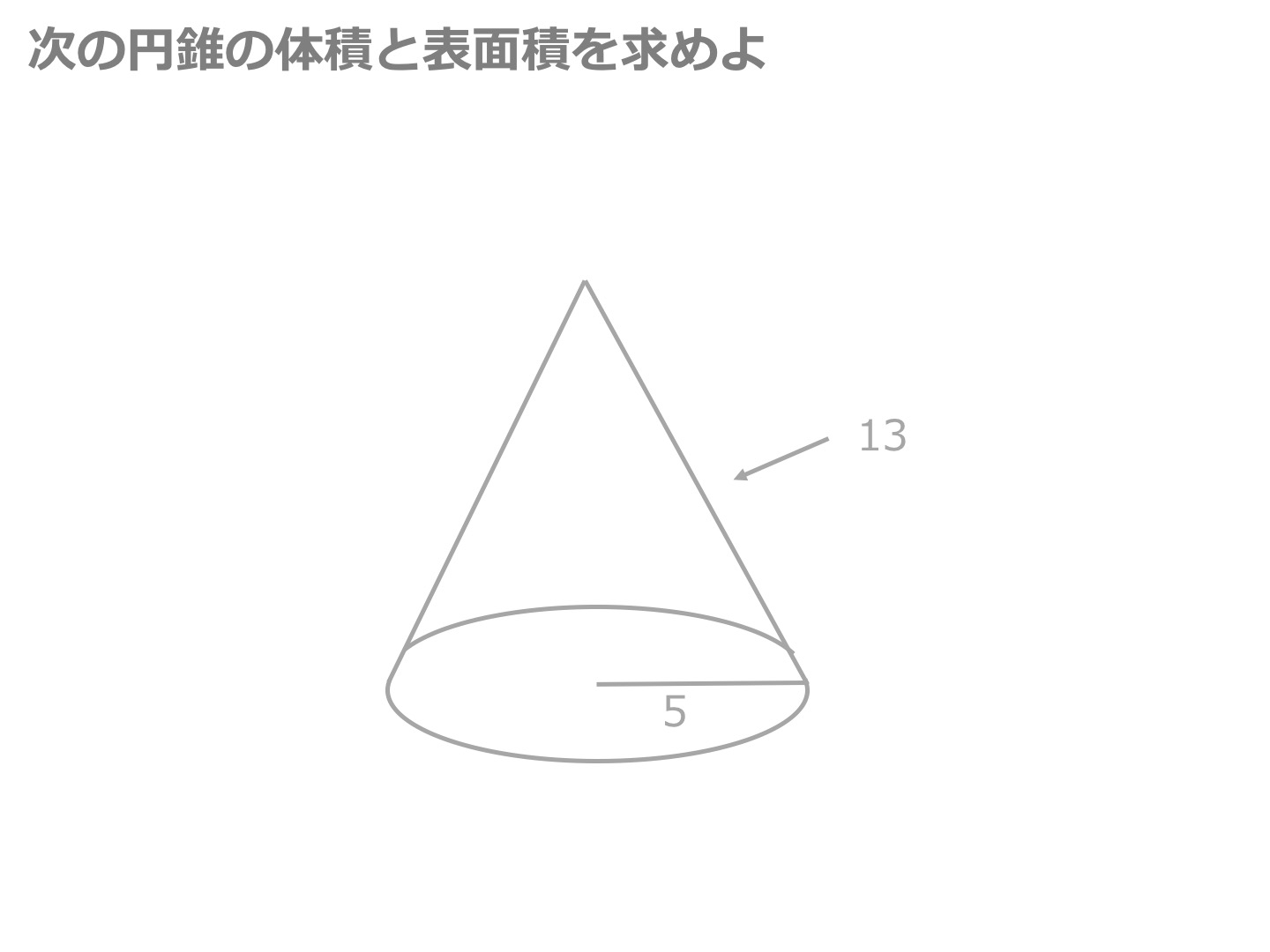



3分でわかる 円錐の体積 表面積の求め方 合格サプリ



地図の体積計測




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
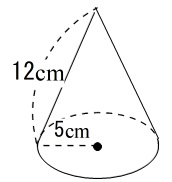



円錐 すい の表面積や四角錐 五角錐の体積の求め方




空間図形14 円すい台の体積 Youtube




円錐の体積の求め方 公式 小学生 中学生の勉強




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
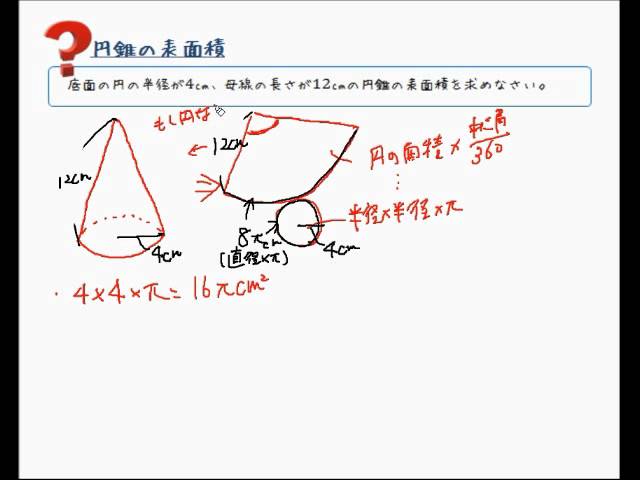



円錐の表面積 Youtube




円錐の体積の求め方 公式と計算例




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




どうして1 3なの 錐の体積の公式の求め方 まなべーと




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
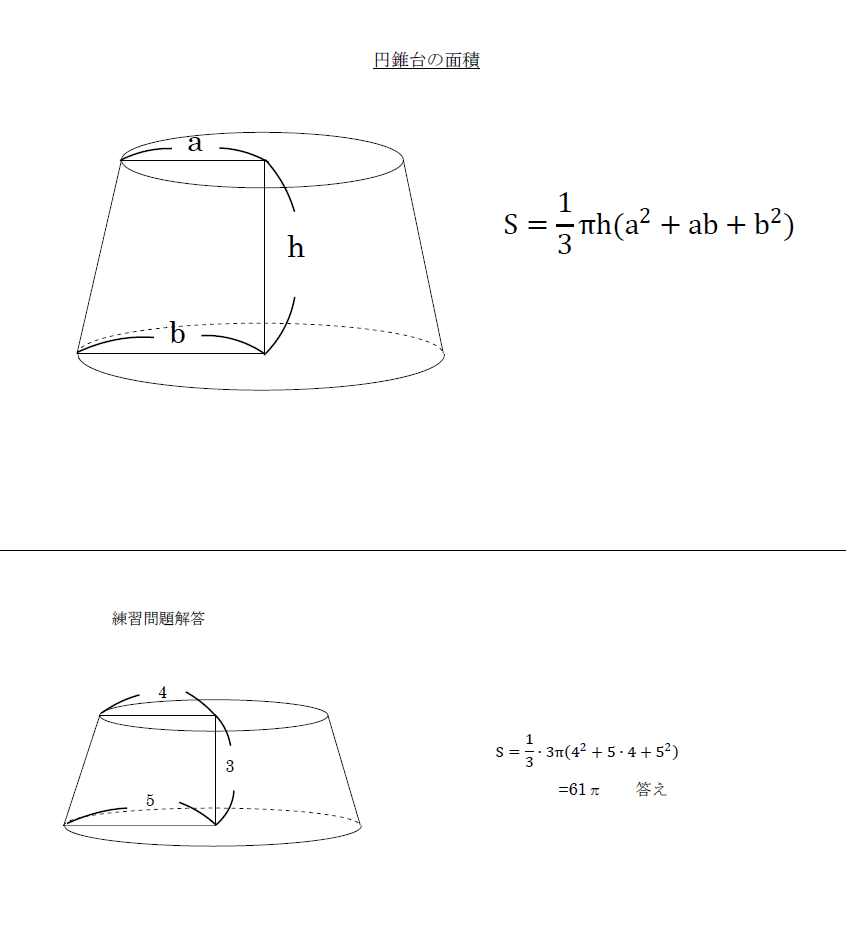



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



Studydoctor円錐や角錐の体積の求め方 中学1年数学 Studydoctor



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear




円錐の表面積 Youtube




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook



1



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor



3




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方



質量と比重




毎日問題を解こう 27 苦手な数学を簡単に
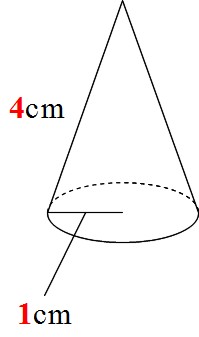



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
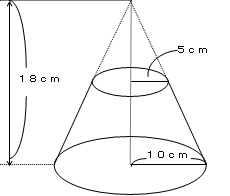



体積 円錐台の体積を求める 子供に教える算数のツボ




公式を図解 すい体の体積 円すいの表面積の求め方



立体の表面積




円錐の表面積の求め方 公式と計算例



立体の体積 V 表面積 S または側面積 F および重心位置 G 直円錐 P12




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo



3




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中3 三角形の相似 円錐の体積比 日本語版 Youtube




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の体積ってなんであの公式なの Webty Staff Blog




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




円錐の体積を求める Youtube




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



中学数学 円すいに関する練習問題




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐の表面積を 公式を使って求める チーム エン




角錐 円錐の体積と表面積の公式 数学fun



1



円錐の体積の求め方を教えてください 底面の直径と母線の長さがともに8c Yahoo 知恵袋




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
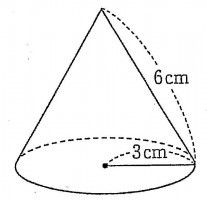



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




高校入試対策数学 円錐に関する対策問題 Pikuu




球の体積と表面積 公式と計算問題と証明 Irohabook



写真の円錐の体積と表面積を求める問題なんですが この答えであっているでしょ Yahoo 知恵袋
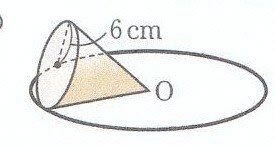



円すいの表面積を求める 数友で入試問題を解こう 2 べんきょうなせん W




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




50 円錐 の 体積 求め 方 最高のぬりえ




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト
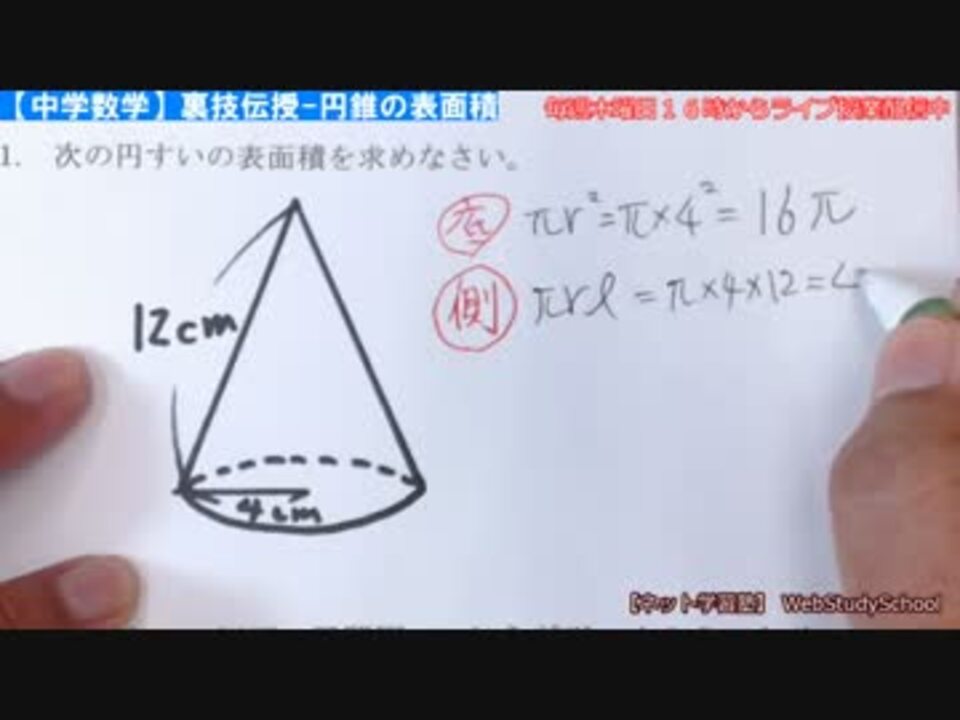



Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ
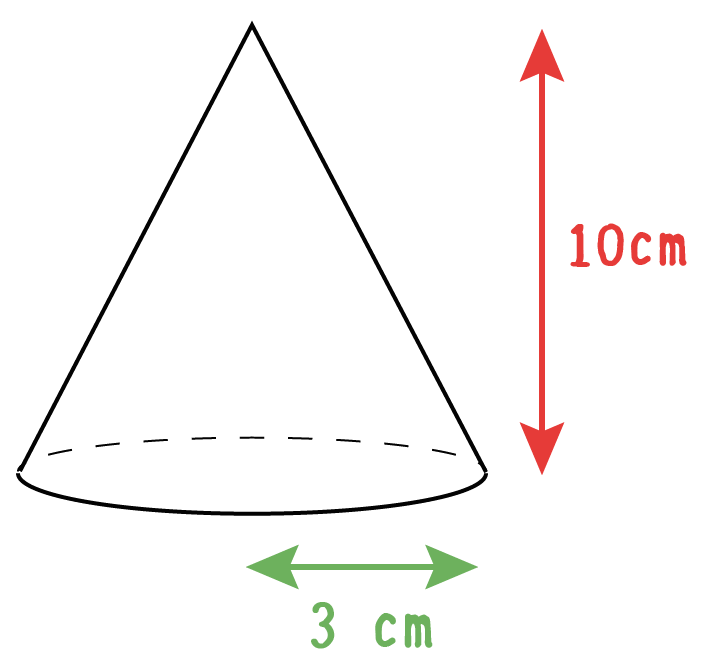



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
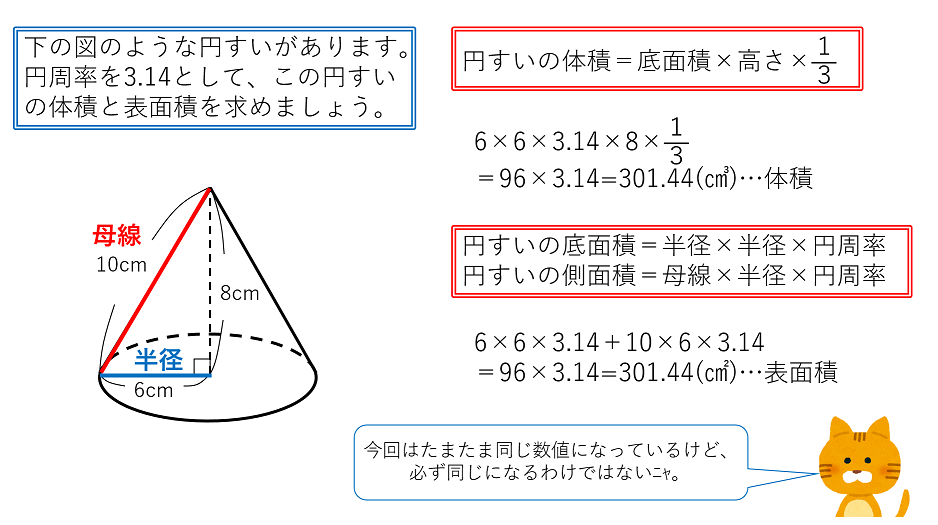



五角錐数 Pentagonal Pyramidal Number Japaneseclass Jp




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




ม 1 โน ตของ 中1数学 円錐の表面積のポイント ช น Junior Clear




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




直円錐を平面で切ったとき 分断される部分の体積と表面積 特殊相対性理論 電磁気学 数学




高さの分からない円すい展開図 どうやって立体の体積を求めるの



0 件のコメント:
コメントを投稿