Get answer If y=cos^(1)((2^x1),(14^x), find (dy),(dx) Apne doubts clear karein ab Whatsapp par bhi Try it now tan1 x = y x= tany 2tan1 x= cos1 1x 2 /1x 2 = cos1 1tan 2 y/1tan 2 y = cos1 (cos2y) =2y =2tan1 x therefore, 2tan1 x = cos1 1x 2 /1x 2Questions from Continuity and Differentiability 1 The derivative of tan − 1 ( 2 x 1 − x 2) with respect to cos − 1 1 − x 2 is KEAM 09 2 If r = a e θ cot α where a and α are real numbers, then d 2 r d θ 2 − 4 r C o t 2 α is ____ KCET 11

The Derivative Of Cos 1 2x 2 1 W R T Cos 1 X Is
Y=cos^(-1)(2x sqrt(1-x^(2)))
Y=cos^(-1)(2x sqrt(1-x^(2)))-Y = cos ( 1/2 x) y = cos ( 1/3 x) We can see that in fact, B does affect the period of the curve It takes 1/B times to complete a period of a curve If B is equal to 1, then it takes 2pi to complete a period y = cos (x 2) Automatically we can see that the actual picture of the graph does not change, it only shifts If C is positive itLet y = cos − 1 (2 x 1 − x 2 ) Put x = sin θ ∴ θ = sin − 1 x ⇒ y = cos − 1 (2 sin θ 1 − sin 2 θ) ⇒ y = cos − 1 (2 sin θ cos θ) ⇒ y = cos − 1 (sin 2 θ) ⇒ y = cos − 1 cos (2 π − 2 θ) ⇒ y = 2 π − 2 θ ⇒ y = 2 π − 2 sin − 1 x ⇒ d x d y = 1 − x 2
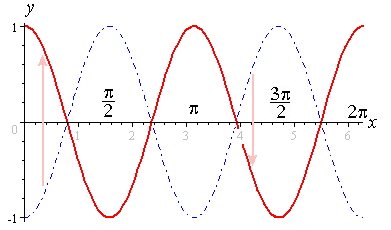



3 Graphs Of Y Asin Bx C And Y Acos Bx C
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!COMEDK 08 If y = sin1 ((5x12 √1 x2/13)) , then (dy/dx) = (A) (3/√1 x2) (B) (12/√1 x2) (1/√1 x2) (D) (1/√1 x2) Check AIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;
Graph y=cos(1/2x) Use the form to find the variables used to find the amplitude, period, phase shift, and vertical shift Find the amplitude Amplitude Find the period of Tap for more steps The period of the function can be calculated using Replace with in the formula for periodQuestion Differentiate Each Of The Functions Below 6 Y(x) 2(cos1 X)2 7 R(p) 27 Tan11p 8 Y(x) = Cos1 (2x 1) Tan(2x 1) 9 Y(y) = Cos1 Tan (2x 1) If y = cos^(1) ((2x)/(1 x^(2))), 1 lt x lt 1 " then " (dy)/(dx) is equal to Updated On 132 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!
The Chain Rule, when applied to the cosine, tells us that if u is some function in terms of x, d dx cosu = − sin(u) ⋅ du dx Here, we see u = 1 − e2x 1 e2x du dx can be calculated with the Quotient Rule and the Chain Rule for exponentials, which tells us that d dx eax where a is some positive constant is given by aeaxIntegrate 1/(cos(x)2) from 0 to 2pi;Volume y=x1, y=0, x=0, x=2 \square!




Cos 2x




If Y Cos 1 2 X 1 1 4 X Find Dy Dx
Figure 684 shows the graph of y = 2 cosh (x / 2) y = 2 cosh (x / 2) Figure 684 A hyperbolic cosine function forms the shape of a catenary Example 651 Using a Catenary to Find the Length of a Cable Assume a hanging cable has the shape 10 cosh (x / 10) 10 cosh (x / 10) for −15If Cos 1 2x 2 1 2pi 2cos 1 X Then Youtube For more information and source, see on this link https//wwwyoutubecom/watch?v=pWI3kXyZvpsWe need to find domain of $$\cos^{1} \frac{2x1}{2\sqrt2x}$$ The way I did it was by solving the inequality $ 1\ge \frac{2x1}{2\sqrt2x}\ge1$ And after some grunt work I found the answer but the answer key says the domain is just ${\frac12}$ After some conformations, I got to know that the answer key is right so I rechecked my inequality and got the same answer which is different from




If Cos 1 2x 2 1 2pi 2cos 1 X Then Youtube
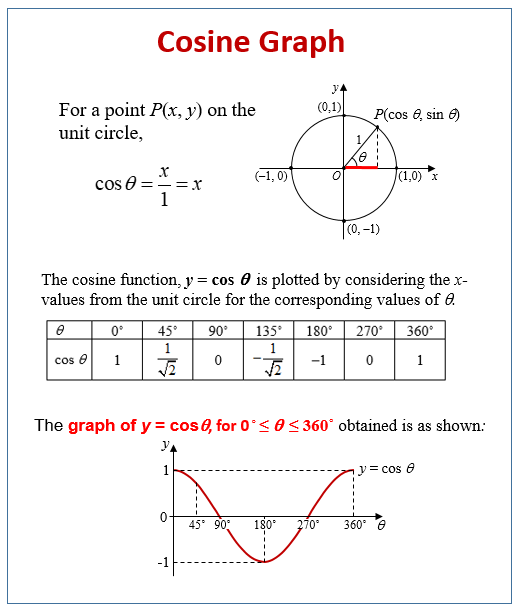



Cos Graph Solutions Examples Videos
1answer Find dy /dx y = cos ^1 (2x /1x^2 ),1 < x < 1 askedin Mathematicsby sforrest072(128kpoints) continuity and differntiability class12 0votes 1answer If x = a(cos t t sin t) and y = a(sin t t cos t) then find the value of d^2x/dy^2 at t = pi/4Integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;Put `x=sintheta` `theta =sin^1x` `=cos^1 (2sinthetasqrt (1sin^2theta))` `=cos^1 (sin2theta)` `=cos^1 (cos (pi/22theta))` `y=pi/22theta=pi/22sin^1x` Differentiating with respect to 'x', we get `dy/dx=0 2/sqrt (1x^2) = (2)/sqrt (1x^2)`




Limit Of 1 Cos X X As X Approaches 0 Video Khan Academy




Ipe Material Notes
The inverse trigonometric identities or functions are additionally known as arcus functions or identities Fundamentally, they are the trig reciprocal identities of following trigonometric functions Sin Cos Tan These trig identities are utilized in circumstances when the area of the domain area should be limited These trigonometry functions have extraordinary noteworthiness in EngineeringPiece of cake Unlock StepbyStep y = cos²(2x 1) y = 1/2 1/2cos2(2x 1) y = 1/2 1/2cos(4x 2) dy/dx = 1/2sin(4x 2)(4) = 2sin(4x 2) d²y/dx² = 2cos(4x 2)(4) = 8cos(4x 2)




Y Cos 1 5x 9 A 45x Squareroot 1 25x Y Chegg Com




Tangente Del Angulo Medio Importante Aidentidades Trigonometricas
y = cos1 2 tan θ 1 tan 2 θ Now, using the property sin 2 θ = 2 tan θ 1 tan 2 θ , we get y = cos 1 sin 2 θ y = cos 1 cos π 2 2 θ y = π 2 2 θHere is an example Example 1 Evaluate cos 1 (1/2) If y = cos 1 (1/2), then cos y = 1/2 This equation has an infinite number of solutions, but only one of them is in the range of cosGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
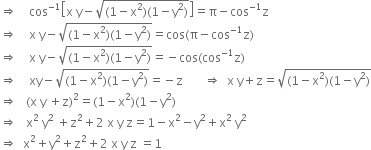



If Cos 1x Cos 1y Cos 1z P Prove That X2 Y2 Z2 2 X Y Z 1 From Mathematics Inverse Trigonometric Functions Class 12 Cbse




Trigonometric Formula Logical Maths And G Knowledge Tips Facebook
Question 1 2x 3y = sinx Solution 2x 3y = sinx Differentiating wrt x, \(23\frac { dy }{ dx } =cosx \) ⇒ \(\frac { dy }{ dx } =\frac { 1 }{ 3 } (cosx2)\) Ex 53, 11 Find 𝑑𝑦/𝑑𝑥 in, 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) , 0 < x < 1 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) Putting x = tan θ y Find the value of tan1/2sin −1 2x/1x 2 cos −1 1−y 2 /1y 2,x0 and xy




Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube




Circunferencia Trigonometrica
Solve For X Cos 1 X 2 1 X 2 1 1 2tan 1 2x 1 X 2 2pi 3 Youtube For more information and source, see on this link https//wwwyoutubecom/watch?v=YenRWf4BqS4X^2 2 y^2 = 1 WolframAlpha Volume of a cylinder? Find the following limit $\lim_{x\to 0}\frac{\sqrt3{1x}1}{x}$ and $\lim_{x\to 0}\frac{\cos 3x\cos x}{x^2}$ 0 Find the smallest positive value of x for which the gradient is




Gambarkan Grafik Fungsi Trigonometri Cos 1 2 X Brainly Co Id
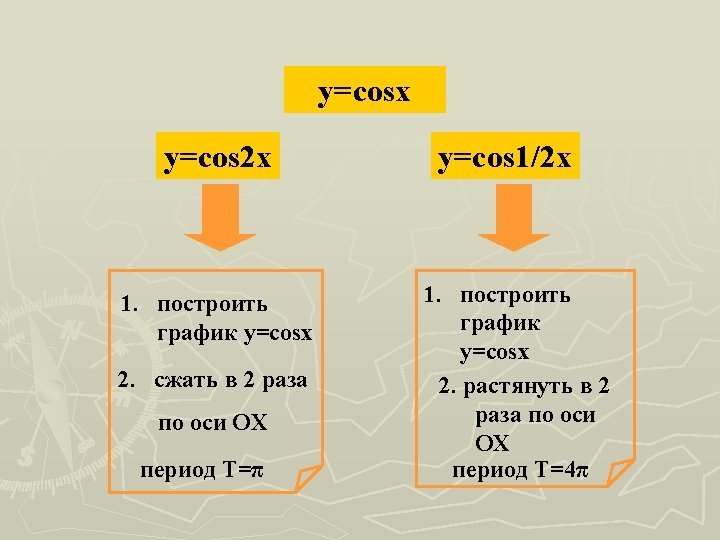



S O C Y Cosx Ysi X 2
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIf y = cos 1 (2x/1x 2), then dy/dx is equal to Put x = => Hence y = So for all xIf ` y= ( cos x ^(2))^(2) , "then" (dy)/(dx) ` is equal to




Calameo Ejercicios Resueltos Ecuaciones Diferenc




If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube
Graph y=2cos (1/2x) y = 2cos ( 1 2 x) y = 2 cos ( 1 2 x) Use the form acos(bx−c) d a cos ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 2 a = 2 b = 1 2 b = 1 2 c = 0 c = 0 d = 0 d = 0 Find the amplitude a a Amplitude 2 2If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube For more information and source, see on this link Ex 5 3 13 Find Dy Dx In Y Cos 1 2x 1 X2 Ncert Ex 5 3 For more information and source, see on this link If Y Cos M Cos 1 X Show That 1 X 2 Y X Y M 2 Y 0Let y = cos 1 √ (1 cos x)/2 We know 1 cos x = 2 cos 2 (x/2) So y = cos 1 √ (2 cos 2 (x/2)/2) = cos 1 √cos 2 (x/2) = cos 1 cos (x/2) = x/2 So dy/dx = 1/2 Hence option (2) is the answer




Y Cos 1 2x 1 X 2 Novocom Top



If Y Cos 1 2x 3 1 X 2 13 Then Find Dy Dx Sarthaks Econnect Largest Online Education Community
View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn more about StepCos (x)= 1/2 \square!Watch Video in App This browser does not support the video element 453 k 431 k Answer Step by step solution by experts to help




Ycos 1 Dfrac2x1x2 1x1 See How To Solve It At Qanda




Derivative Rules For Trigonometric Functions
Get an answer for '`y = cos((1 e^(2x))/(1 e^(2x)))` Find the derivative of the function' and find homework help for other Math questions at eNotes Search this site Go iconquestion Evaluating y = cos 1 x Evaluating cos 1 x expressions follows the same procedure as evaluating sin 1 x expressionsyou must be aware of the domain and range of the function! dy/dx=2x1/sqrt(1x^2) The derivative of y will be the sum of the derivatives of x^2 and cos^1x We will find these separately DERIVATIVE OF bb(x^2) Since you're expected to find the derivative of cos^1x, it's likely you already know how to differentiate x^2 In case you've forgotten, you'll need the power rule




Identidades Trigonometricas
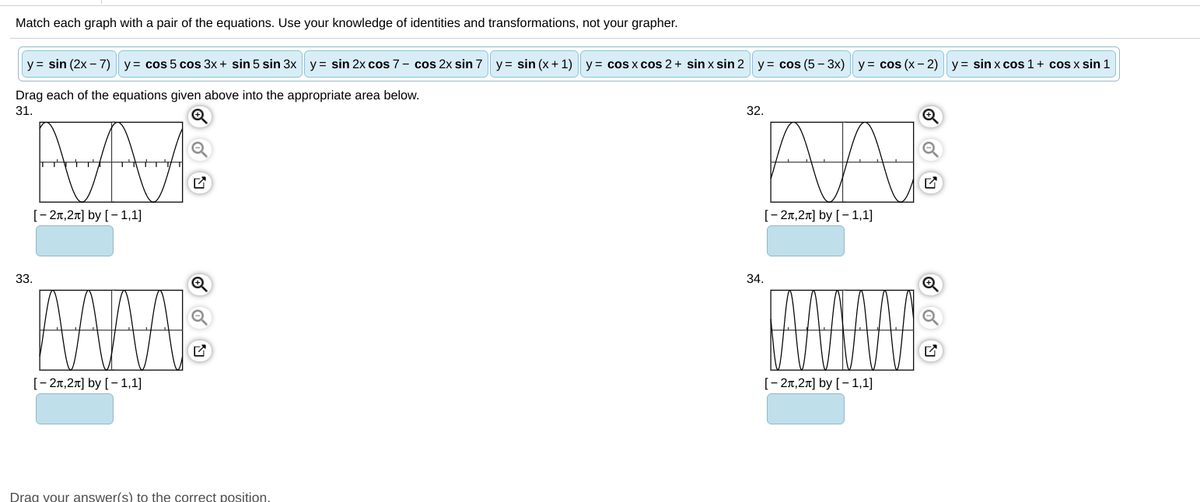



Answered Match Each Graph With A Pair Of The Bartleby
Cosine function, cosx We are finding the cosine of x2, not simply the cosine of x We call such an expression a 'function of a function' if y = cos 1 2 1x2 g) 1 cosx h) 1 x2 2x1 3 Find the derivative of each of the following a) ln sin2 xIf y = cos 1 (2x/1x 2), then dy/dx is equal to Put x = => Henc If y = cos1(2x/1x2), then dy/dx is equal to A for all x < 1 B for all x > 1 C for all x < 1 D None of the aboveSin (θ), Tan (θ), and 1 are the heights to the line starting from the x axis, while Cos (θ), 1, and Cot (θ) are lengths along the x axis starting from the origin The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions



If Y X Cos 1 X 1 X 2 Log 1 X 2 Then Prove That Dy Dx Cos 1 X 1 X 2 3 2 Sarthaks Econnect Largest Online Education Community




A Sec X Y Berkeley City College
But if x is given y has many values We can express y interms of x as y = sin –1 x "Inverse sine of x" The Quantities sin –1 x, cos –1 x, tan –1 x, cot –1 x, sec –1 x, cosec –1 x are called Inverse Trigonometric Functions আবিষ্কার (dy)/(dx) নীচেরতে y=cos^(1)((2x)/(1x^2)),1The given relationship is `y = cos^(1) ((2x)/(1x^2))` `y = cos^(1) ((2x)/(1x^2))`



Www Tau Ac Il Levant Ode Solution 6 Pdf




Ex 5 3 11 Find Dy Dx In Y Cos 1 1 X2 1 X2 Ex 5 3
Get an answer for '`y = cos^1(sin^1(t))` Find the derivative of the function Simplify where possible' and find homework help for other Math questions at eNotesDifferentiate cos(1x^2/1x^2)Differentiate y = cos ( 1 x^2/1 x^2 ) differentiate cos^1(2x/1x^2)cos inverse 1x^2/1x^2 formuladifferentiate cos^1(1xIf you have understood till the third last step,then there is nothing much to understand after that So,the 'y' in the question,arcsin(2x/1x^2) is a little difficult to handle,so a smart substitution has been done in the form of x=tanθ which simp




3 Graphs Of Y Asin Bx C And Y Acos Bx C



Solved Derivative Of Trigonometric And Inverse Trigonometric Functions Find Dy Dx 1 Y Sin X2 3x 1 2 Y Cos 2 2x 1 3 Y Tan Vx2 Course Hero
If y = cos − 1 2 1 x 2 1 x 2 1 , then d x d y is equal to View solution If x = 2 c o s e c − 1 t and y = 2 s e c − 1 t ( ∣ t ∣ ≥ 1 ) , then d x d y is equal toConsider the triangle T ⊂ S with vertices (0,0), (1/2,1/2), (1/2,1) Thus, T is defined by the inequalities 0 < x < y < 2x < 1 For every (x,y) in T, xy > x2 and x2 y2 < 5x2 Show that all solutions of y'= \frac {xy1} {x^21} are of the form y=xC\sqrt {1x^2} without solving the ODE Show that all solutions of y′ = x21xy1 Ex 53, 13 Find 𝑑𝑦/𝑑𝑥 in, y = cos–1 (2𝑥/( 1 𝑥2 )) , −1 < x < 1 𝑦 = cos–1 (2𝑥/( 1 𝑥2 )) Let 𝑥 = tan𝜃 𝑦 = cos–1 ((2 tan𝜃)/( 1 𝑡𝑎𝑛2𝜃 )) 𝑦 = cos–1 (sin 2θ) 𝑦 ="cos–1" (〖cos 〗(𝜋/2 −2𝜃) ) 𝑦 = 𝜋/2 − 2𝜃 Putting value of θ = tan−1 x 𝑦 = 𝜋/2 − 2 〖𝑡𝑎𝑛〗^(−1) 𝑥 Si




How To Graph Cos X Video Lesson Transcript Study Com




Aplicacion De La Derivada Con Rectas Tangentes Y Normales Tangente Pendiente
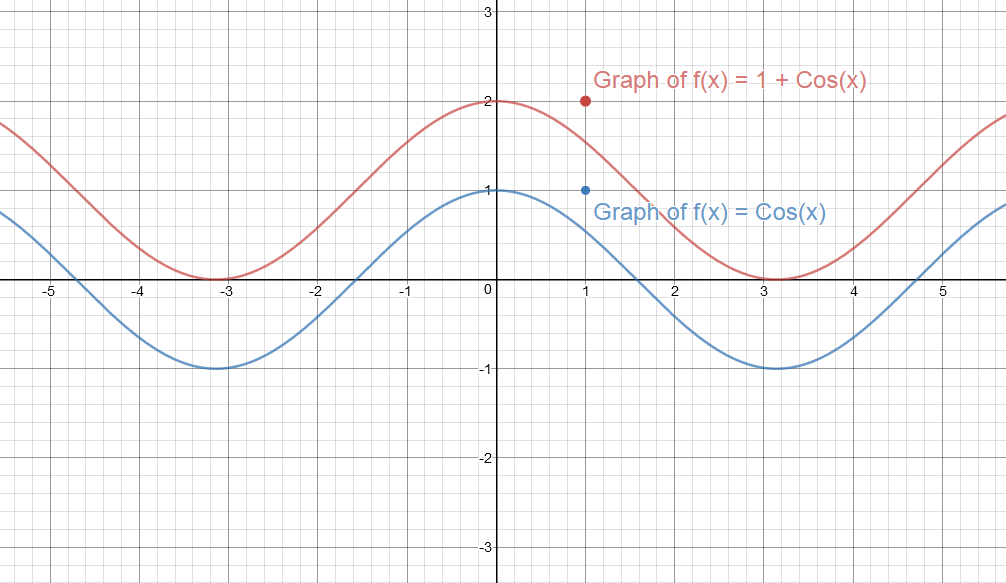



How Do You Graph F X 1 Cosx Socratic




The Derivative Of Cos 1 2x 2 1 W R T Cos 1 X Is




If Y Cos 1 X Find D 2y Dx 2 In Terms Of Y Alone Mathematics Shaalaa Com



Http Www Eco Uc3m Es Docencia Matematicasii English Exercises I Problemas3 Sol Pdf




Rd Sharma Solutions For Class 12 Maths Chapter 4 Inverse Trigonometric Functions Avail Free Pdf



How To Solve Cos 1 2x 1 Quora




Differentiate Sin 1 2x 1 1 4x Wrt X Mathematics Topperlearning Com P8672lhh




Solved 1 Find The Derivative Of Y Cos 1 X2 A O 2x 2 Chegg Com




The Cosine Function Functions Siyavula



Solve The Following For X Cos 1 X 2 1 X 2 1 Tan 1 2x X 2 1 2p 3 Sarthaks Econnect Largest Online Education Community



Www Guao Org Sites Default Files Suma y resta de seno y coseno de angulo doble Pdf




Find The Value Of Cot1 2 Cos 1 2x 1 X2 Sin 1 1 Y2 1 Y2 Maths Inverse Trigonometric Functions Meritnation Com




Y Ex Cos X Sin X 0 1 Novocom Top




Rd Sharma Solutions For Class 12 Maths Chapter 4 Inverse Trigonometric Functions Avail Free Pdf




If Y Cos 1 2x 1 X 2 Then Find Dydx
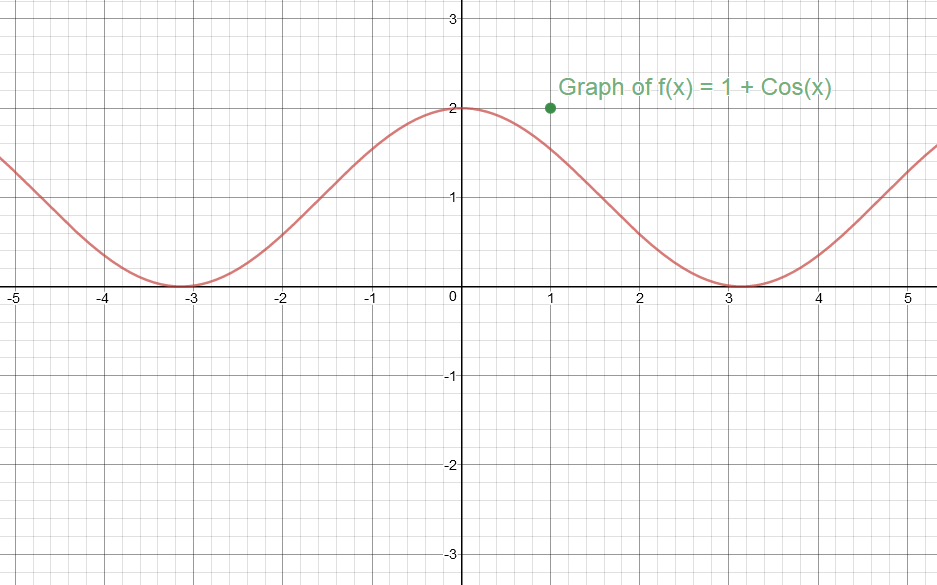



How Do You Graph F X 1 Cosx Socratic




Aim What S The A In Y A Sin X All About Ppt Video Online Download



Www3 Nd Edu Apilking Math Work Old exams Exam 3f12 Sols Pdf




Math Trigonometry All Formula Math Formula



Properties Of Graphs Of Trigonometric Functions Opencurriculum




If Y Cos 1 2 X 11 4 X Then Find Dydx
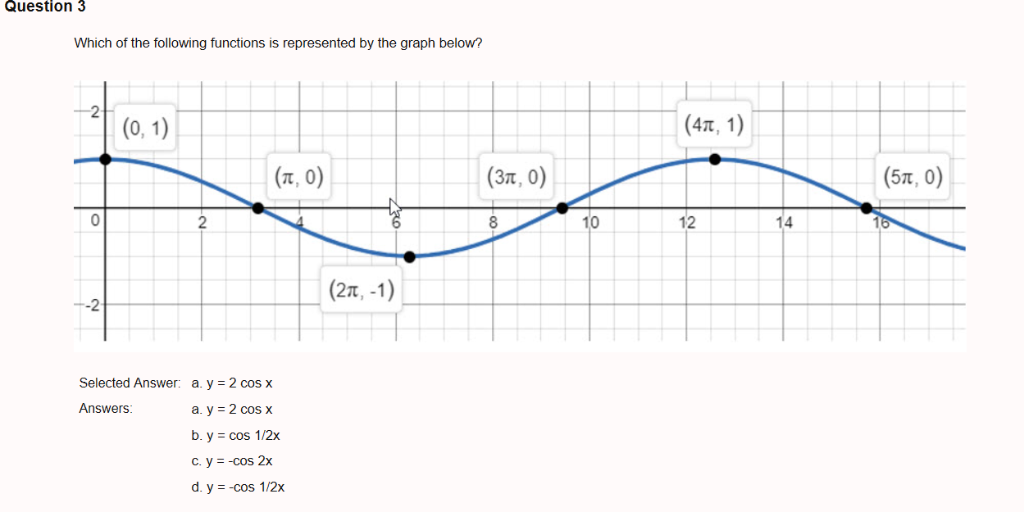



Question 3 Which Of The Following Functions Is Chegg Com




Ex 5 3 11 Find Dy Dx In Y Cos 1 1 X2 1 X2 Ex 5 3




Hw 13




Solution Please Someone Help Me Find The Derivative Of Y Cos 1 3 2x




If Y Cos 1 2x 1 X 2 Then Dy Dx Is Equal To




Yleq1 And Xygeq0 Then X2zpiwh See How To Solve It At Qanda



If Y Cos 1 2 X 1 1 4 X Fin Dy Dx Sarthaks Econnect Largest Online Education Community



2



If Y Cos 1 2x 3 1 X 2 13 Then Find Dy Dx Sarthaks Econnect Largest Online Education Community




1 Cos 4 X Sinº X Cos 2x 6 6 2 Sin X Cos X Homeworklib



The Inverse Cosine Function




Ejercicios Con Ecuaciones Trigonometricas Superprof




Iit Jee 19 Mains On Sin 1 Sinx And Cos 1 Cosx Offered By Unacademy




Prove That Cos X Ge1 2x Over Pi Forall X In 0 Pi Over2 Mathematics Stack Exchange




Ejercicios Con Ecuaciones Trigonometricas Superprof



Y Cos 1 8x 4 8x 2 1 Prove That Dy Dx 4 1 X 2 1 2 Askiitians



How To Differentiate Y Tan 1 2x 1 X 2 For The Inverse Trigonometric Function Quora




Funcion Trigonometrica Inversa Monografias Com




Ex 5 3 15 Find Dy Dx In Y Sec 1 1 2x2 1 Chapter 5



Http Aimpointsiwan Com Qb Inverse trigonometric Pdf



How Do You Graph Y 1 2 Cos 2x Socratic




Domain Of Function Cos 1 2x 1 Mathematics Topperlearning Com 9bg6o4aa




Ex 5 3 13 Find Dy Dx In Y Cos 1 2x 1 X2 Ncert Ex 5 3




यद Y Cos 1 2x 2cos 1 Sqrt 1 4x 2 द ख ए क Dy Dx 2 Sqrt 1 4x 2 Youtube
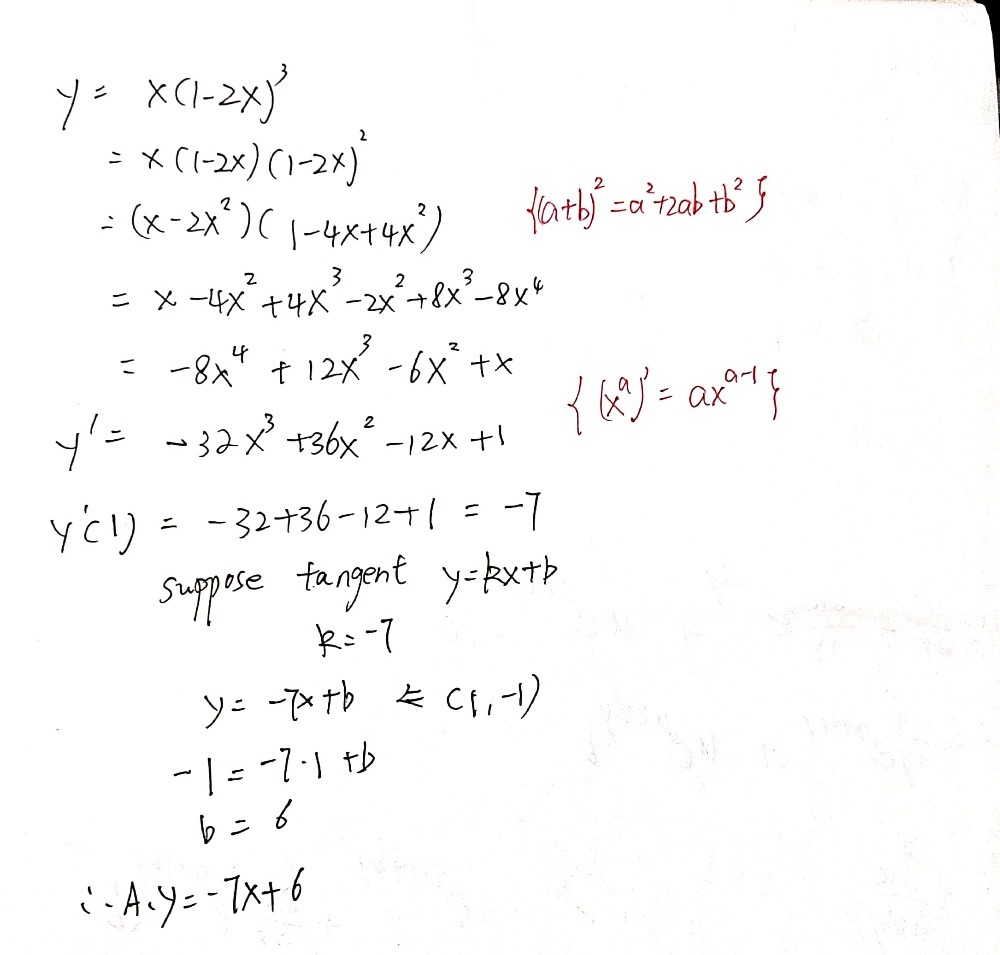



1 Cos 2x 1 Cos X Cos 1x2 An Equation Of The Tang Gauthmath




If Y Cos 1 2x 1 X 2 1 Lt X Lt 1 Then Dy




Soluciones Derivadas




Ejercicios Resueltos De Calculo De Derivadas




43 If Y Cos 1 2x 2 Cos 1 Rootover 1 4x2 1 2 Lessthan X Lessthan 0 Find Maths Continuity And Differentiability Meritnation Com
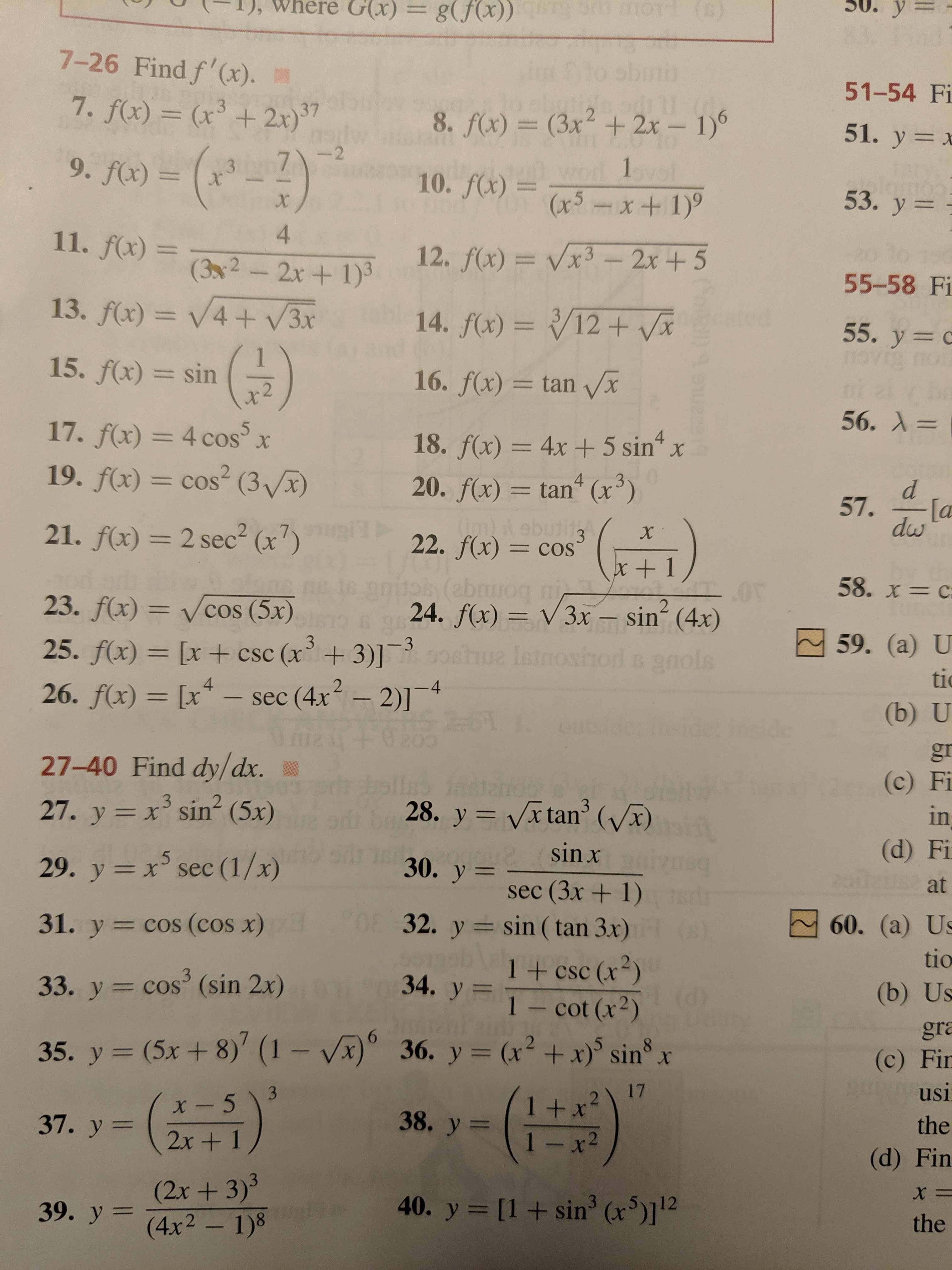



Answered G X U G Fx 00 O 7 26 Find F X Bartleby




Y Cos 1 3x 4 Sqrt 1 X 2 5 Simplify Calculator



What Is The Value Of Math Cos 1 2x 1 Math Quora




Find Dx Dy For Y Cos 1 2x 1 X 2 1 X 1 Mathematics Shaalaa Com




Differentiate Tan 1 1 X2 1 2 1 X Wrt Sin 1 2x 1 X2 Explain In Great Detail Mathematics Topperlearning Com Yx862gdd




Ejercicios Resueltos Y Propuestos De Derivadas Studocu
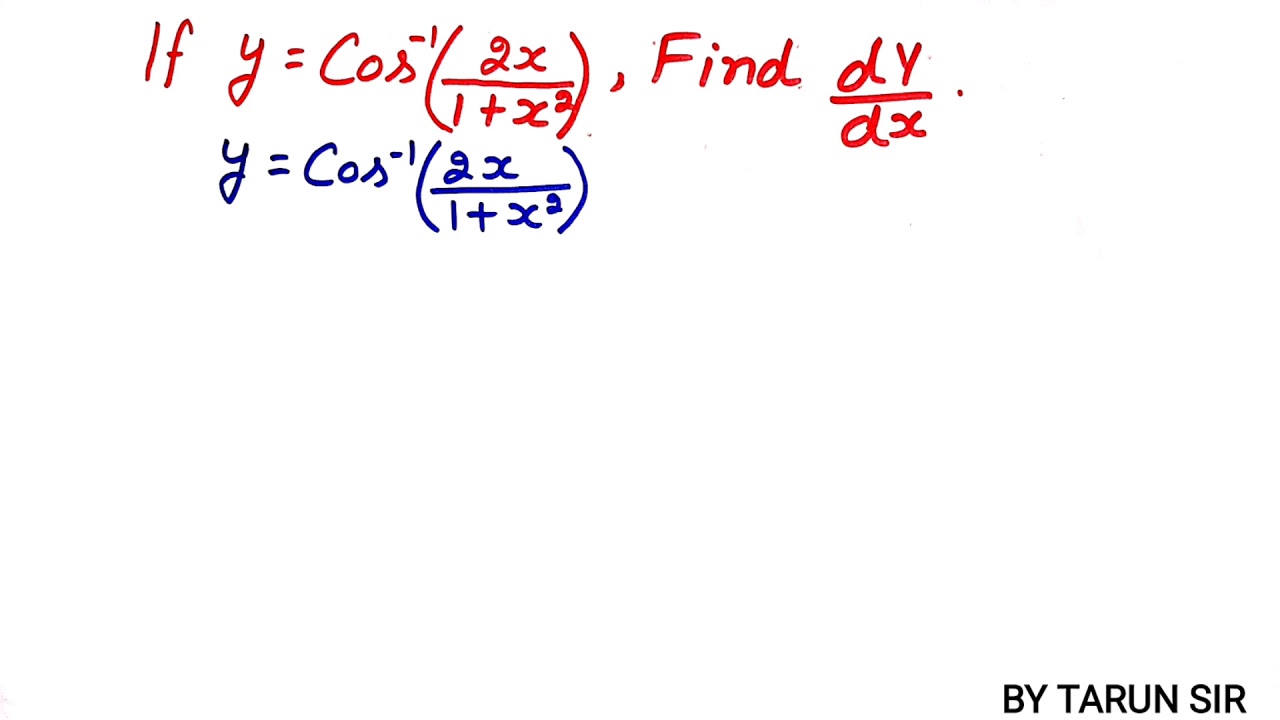



Find Differentiation Of Cos Inverse 2x 1 X 2 Youtube
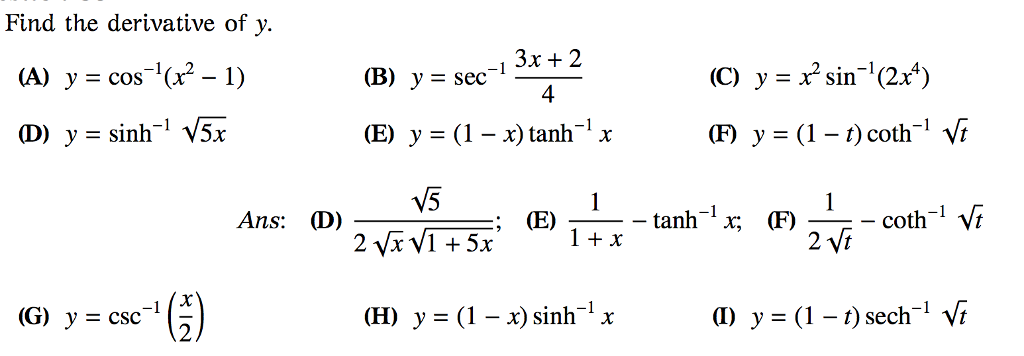



Find The Derivative Of Y A Y Cos 1 X 2 1 Chegg Com




46 If Y Cos 1 Left Frac 2 X 3 Sqrt 1 X 2 Sqrt 13 Right Find Frac D Y D X




Tan11 Example 7 Show That I Sin 1 2x V Sin 1 2x 11 X2 2




Y 3 Cos 1 2x Novocom Top



Cos 2x 1 的导数是什么 Y Cos 1 2x 怎么求导



F X X Cos 1 X If X 0 At X 0 If X 0 Studyrankersonline




If Y Cos 1 2x 3 1 X 13 Find Dy Dx Brainly In




Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2




Ipe Material Notes
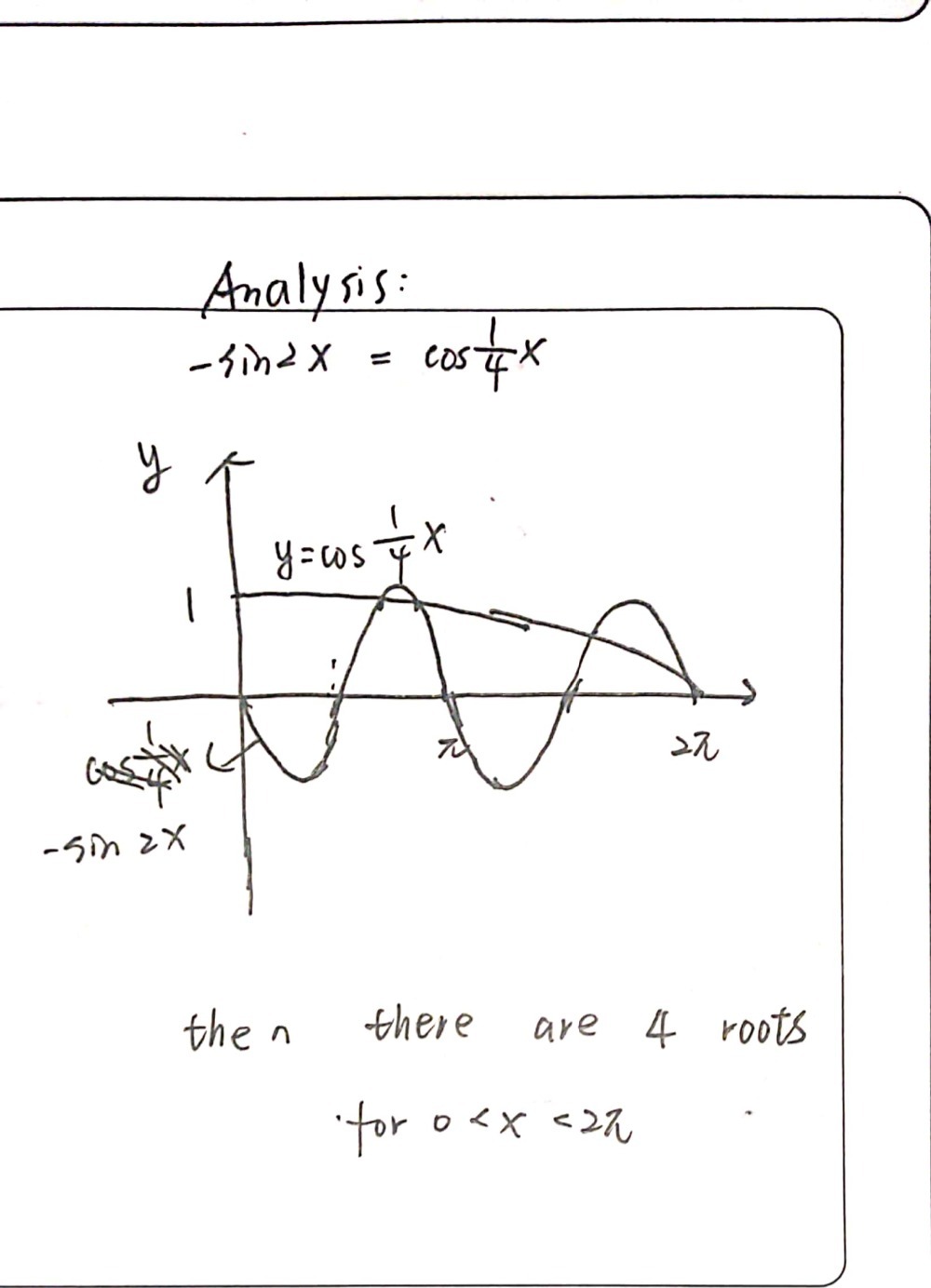



Y Sin 2x And Y Cos 1 4 X For The Domain 0 Q X Gauthmath
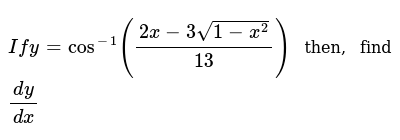



If Y Cos 1 2x 3sqrt 1 X 2 13 Then Find Dy Dx
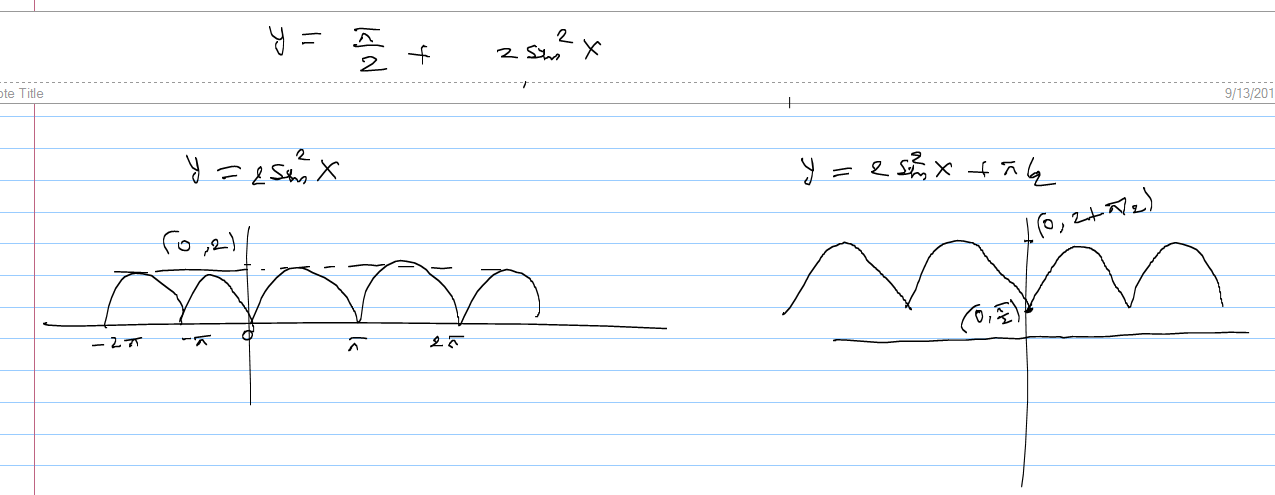



Differentiate W R To X When Y Cos 1 X 2 1 2x 2 Askiitians




Y Cos 1 2x 1 X 2 Novocom Top



0 件のコメント:
コメントを投稿