Six congruent copies of the parabola $y = x^2$ are arranged in the plane so that each vertex is tangent to a circle, and each parabola isWrite an equation for a parabola that is congruent to the graph of y = x2, opens downward, and has its vertex at (3,1) close Start your trial now!The equation of a parabola can be converted into the vertex form y = a(xh) 2 k, where h = xcoordinate of vertex, and k = ycoordinate of vertex Also, if a is positive, the parabola opens upward Also, if a is positive, the parabola opens upward
Parabola Knowino
Parabola congruent to y=x^2
Parabola congruent to y=x^2-The vertex form of the equation of the parabola is given by {eq}y=a(xh)^2k {/eq} For the parabola to be congruent to the given parabola, {eq}a=\dfrac{1}{2} {/eq}Transcribed image text 1 point 17) Which equation describes a parabola that opens downward, is congruent to y = x*2, and has its vertex at (0, 3)?



Quadratic Function
Since it is so simple to find the yintercept (and it will probably be a point in my Tchart anyway), they are only asking for the xintercepts this timeTo find the xintercept, I set y equal 0 and solveY = (x 3)2 1 y = – x2 3 B) y = (x – 3)2 yAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
There are two forms of Parabola Vertex Form The Vertex form of the quadratic equation of Parabola is y = (x – h)2 k, here (h,k) are the points on the xaxis and yaxis respectively As we have seen Parabola has two different forms of equations The method to find Vertex is different for both forms of equationsWrite the Equations of Parabolas Example Write the equation of a parabola that is congruent to y = 3x 2, has a maximum value of 10, and an axis of symmetry of x – 8 = 0 Write the answer in the form y = ax 2 bx c Write the Equation in Vertex Form Although the question asks for the equation to be written in standard form, we always begin with vertex form y = a(x – p) 2 q ToQuestion Hand 9 Write The Equation For Each Parabola With The Given Information Mark Each A) Congruent To Y = 2x Opens Up, With A Vertex Of (51) > Congruent To Y =(x 2), Maximum Vukue Of 4, Equation Of Asis Of Symmetry * = 2 10 Write The Equation Of The Parabola With Given Vertex, If It Passes Through The Given Pointcz A) Vertex (0,1), Passing Through (29)
Consider a parabola P that is congruent (has the same shape) to y=x^2 , opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left Translated 3 units up Reflected in the xaxis and translated 2 units to the right and 4 units downThen the result seems as follows A (xb)^2C Here you know how you derived up to this Then see the part ( x B ) Here, you know that B = b/2a And Sal told that to obtain the vertex form the Part A ( x B )^2 should be equal to zero in both the cases AndIf (a, a 2) falls inside the angle made by the lines y = 2 x and y = 3 x in first quadrant, then a belongs to View solution The tower of a bridge, hung in the form of a parabola, have their tops 3 0 metres above the roadway are 2 0 0 metres apart



1



2
Explain how you know These two parabolas are not congruent They have the same vertex but different values for each in the domain, except for the point ( , ) If we translateThe set of points (x, y) whose distance from the line y = 2 x 2 is the same as the distance from (2, 0) is a parabola This parabola is congruent to the parabola in standard form y = K x 2 for some K which is equal toArrow_forward Question Write an equation for a parabola that is congruent to the graph of y = x 2, opens downward, and has its vertex at (3,1) check_circle Expert Answer



Vertex Form




Algebra Ii Module 1 Topic C Lesson 35 Student Version
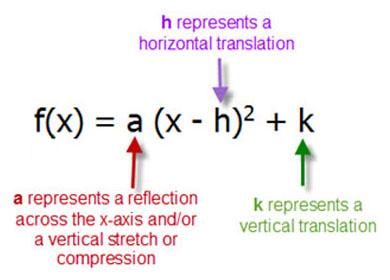
👍 Correct answer to the question The vertex form of the equation of a parabola is y = 2(x 3)2 5 What is the standard form of the equation?Thus, for example, the graph of the parabola with equation y = (x − 3) 2 5 is congruent to the basic parabola, with a shift to the right of 3 units and a shift upwards of 5 units The vertex is at (3, 5) and the axis of symmetry is x = 3 We can find the yintercept by putting x = 0 to give y = 14Suppose the parabola with equation y = 2x^2 undergoes the translation T2,3 Find an equation for its image Vertex form is y k = a(x h)^2 Also given is Th,k, with h = 2 and k = 3 Also given is that a = 2 in the expression 2x^2 Now fill in a, h and k with the given numbers y 3 = 2(x 2)^2 > and there's the answer




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation



How To Graph A Parabola Y 4x 2 Socratic
Foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=3x^{2} en Related Symbolab blog posts Practice, practice, practice Consider a parabola P that is congruent to y=x^2, opens upward, and has vertex (0,0) Find the equation of a new parabola that results if P is reflected in the xaxis, and translated 1 unit to the left and 3 units upThis video solution is related to the Ontario highschool textbook "10 Principles of Mathematics Nelson"
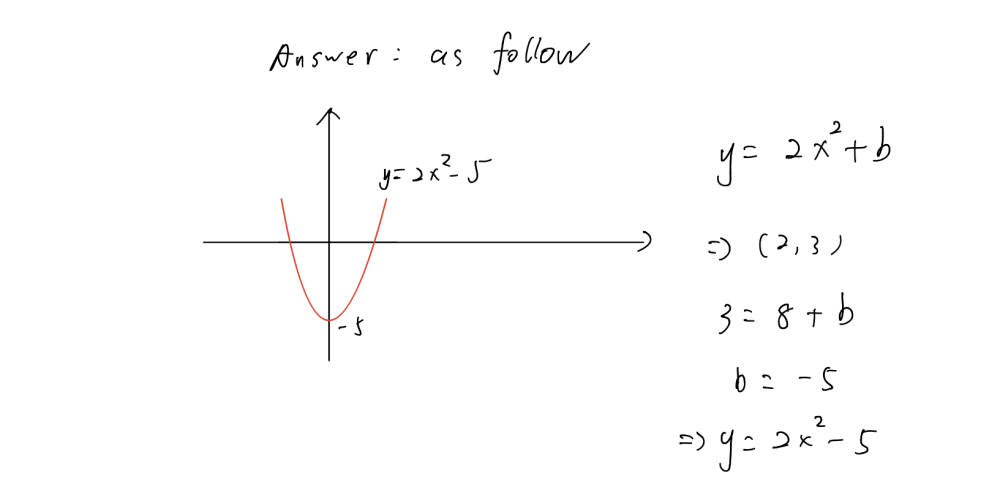



Vrite The Equation Of A Parabola That Matches The Gauthmath



Unique Quadratic Equation In The Form Y Ax 2 Bx C
Therefore, Y^2 = X => Y^2 = 4 (1/4)X ieY^2=4aX, where a=1/4 Clearly it is a left handed parabola Now we know that the vertex of the parabola is at Origin (0,0) ie Y=0 & X=0A parabola is congruent to y=x^2 and has xintercepts 1 and 5 determine the coordinates of the vertex Answer by Fombitz () ( Show Source ) You can put this solution on YOUR website!First week only $499!




5 Consider The Parabola Of The Function P X Below P X 3 6 A Write The Equation Of Homeworklib




How Do You Graph Y X 2 2
We can find the parabola's equation in vertex form following two steps Step 1 use the (known) coordinates of the vertex, ( h, k), to write the parabola 's equation in the form y = a ( x − h) 2 k the problem now only consists of having to find the value of the coefficient a Step 2 find the value of the coefficient a by substitutingIf we put x = 0 we obtain y = 9 and this is called the yintercept The graph of y = (x − 3)2 is congruent to the basic parabola, but is translated 3 units to the right We can confirm this with a table of values Similarly, the graph of y = (x 5)2 is congruent to the basic parabola, but is translated 5 units to the left Its vertex is theSimilarly, the graph of y = (x 5)2 is congruent to the basic parabola, but is translated 5 units to the left Its vertex is the point (–5, 0) and the axis of symmetry is x = –5 0 25 (–5, 0) axis o f s y m metr y (a – 5, a2) y =(x 5)2 x = – 5 x y EXERCISE 1 a Write down the equation of the parabola obtained when the graph of y




Graphing Quadratic Functions



How To Find The Minimum Or Maximum Value Of A Function In Vertex Form
Parabola congruent to y = ax2 xintercepts at x = m and x = n (aka the "zeros" of the quadratic function) Regardless of the form, a parabola opens up when a > 0 and opens down when a < 0, with the axis of symmetry passing through the vertex of the parabolaQuestion Find the equation of the parabola with vertex (4,4), the parabola opens upwards and is congruent to y=1/2x^2 Can you please help me?A parabola is symmetric about the vertex If you take the average of the x intercepts you will find the x coordinate of the parabola




Quadratic Functions Academic Support Center



L2d2ii Html
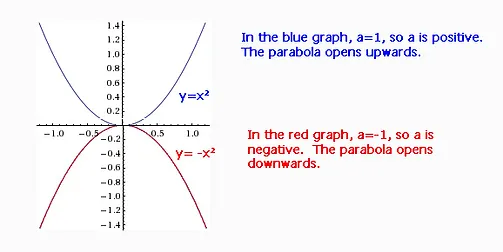
4The trace in the plane y= xsatis es the equation z= x( x) = x2 It is an \upsidedown" parabola, shown in Figure 1614(d) 5The intersection with the coordinate plane x= 0 satis es the equationDesmos offers bestinclass calculators, digital math activities, and curriculum to help every student love math and love learning mathSet y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download




2 Write The New Equation For The Parabola Y X After Chegg Com
$ (x 3)^2 (y 4)^2 = ( 7 x y 25 )^2 / (7^2 1^2) $ Distance of $(3, 4)$ from the directrix is $(21 4 25)/\sqrt{50} = \dfrac{8}{5\sqrt{2} } $ The axis is along the vector $(7, 1)$ , so the vertex is given by math Consider a parabola P that is congruent (has the same shape) to y=x^2 , opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left•Consider a parabola that is congruent to y = 2 x, and with vertex (2, ‐4) Find the equation of a new parabola that results if it is (a) Translated 6 units down (b) Translated 5 units left (c) Translated 6 units up and 5 units right



Solved Write An Equation Of A Parabola That Has A Vertex 3 8 Opens Downward And I Congruent In Shape To The Graph Of Y 5x2 1 The X Interce Course Hero



The Parabola
5 x 2 5 x 2 Set y y equal to the new right side y = 5 x 2 y = 5 x 2 y = 5 x 2 y = 5 x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 5 a = 5 h = 0 h = 0 k = 0 k = 0 Since the value of a a is positive, the parabola opens up1 start by plotting the vertex (if the parabola is congruent to y=x(squared) 2 plot the second point by moving left one unit and up one unit from the last point 3 plot the third point by moving left one unit and up three units from the last point 4 plot mirrored points to get the right half of the parabolaCategories Uncategorized Leave a Reply Cancel reply Your email address will not be published Required fields are marked * Comment Name *



Content Transformations Of The Parabola




2 Marks 4 If The Point 2 7 Is On The Parabola Y Chegg Com
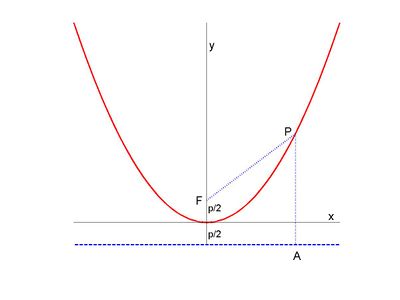
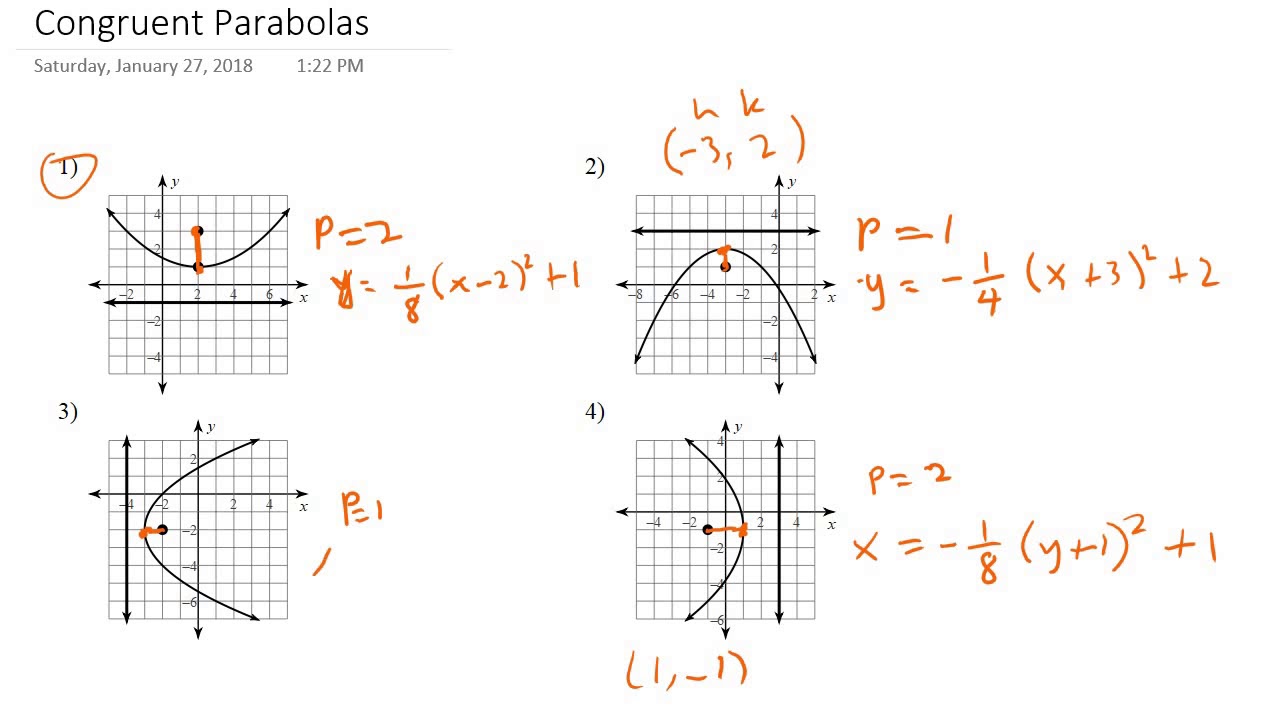
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axisY 2= 2a(x 2hx h) k Square the binomial y = ax2 2ahx ah2 k Use the Distributive Property This is in standard form, with b = –2ah and c = ah2 k With these substitutions, the equation becomes y = ax2 bx c Congruent Parabolas Because the parabola determined by the equation y k = a(x h)2 is a translation image of the2 Given y = 3x2 1) Write the equation of a parabola that contains the point (2, 12) that is congruent to the parabola that is given Describe the series of transformations that would move the given parabola to your parabola 2) Write the equation of a parabola that contains the point (0, 8) that is congruent to the parabola that is given



1



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
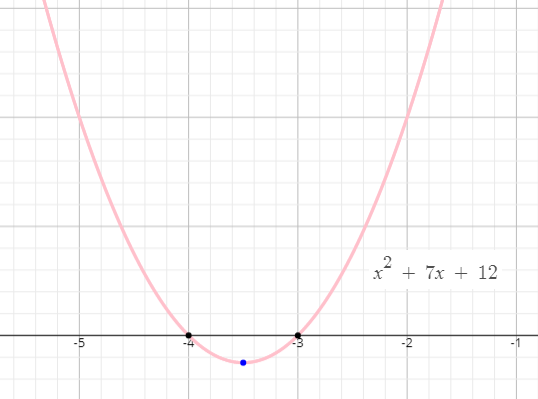
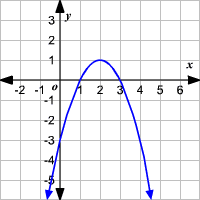
Thanks so much in advance) Found 2 solutions by DrBeeee, josmiceliFind the xintercepts and vertex of y = –x 2 – 4x 2; So p = 2 , q = 3 Given that congruent to y= 2x² and opens down congruent means has the same a value (same shape) of y= 2x² So a = 2, But it opens downSo a = 2 Substitute a = 2 , p = 2 , q = 3 in vortex form y = (2)(x (2))² 3 y = 2(x 2)² 3 The solution is y = 2(x 2)² 3




Answered The Focus Of A Parabola Is 3 5 And Bartleby




Quadratic Function
A hyperbolic paraboloid (not to be confused with a hyperboloid) is a doubly ruled surface shaped like a saddleIn a suitable coordinate system, a hyperbolic paraboloid can be represented by the equation 6 = In this position, the hyperbolic paraboloid opens downward along the xaxis and upward along the yaxis (that is, the parabola in the plane x = 0 opens upward and the parabolaGet an answer for 'Write the equation of a parabola with a vertex of (2,3) that opens downward and is congruent to y=1/3x^2 ' and find homework help for other Math questions at eNotes Write the new equation of the parabola y = x2 if a) it undergoes a horizontal translation of 3 units left and a vertical translation 4 units down and is congruent to y = 7x?



Congruent Parabolas Youtube




Quadratic Functions Academic Support Center
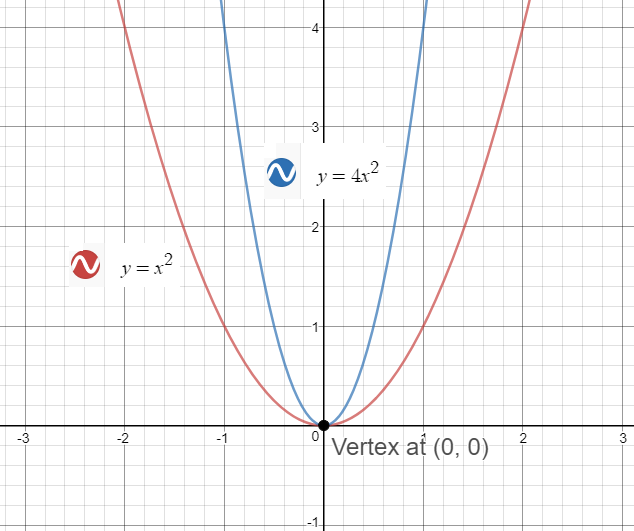
Explanation Parabola described by y = 2x2 is narrower than the parabola described by y = x2 Smaller the coefficient of x2 wider the curveThe equation of the parabola comes out to be y2= 4px where the directrix is the verical line x=p and the focus is at (p,0) parabola "opens to the right" and if p 0 the parabola "opens to the left" The equations we have just established are known as the standardTransformed first parabola coincides with the original second parabola, then the two original parabolas are congruent c Are the two parabolas from part (a) congruent?




Consider A Parabola P That Is Congruent To Y X2 An Gauthmath




What Is The Equation Of A Parabola That Opens Upward And Has X Intercepts At 2 0 And 6 0 Homeworklib




Graphs Of Quadratic Functions Ck 12 Foundation
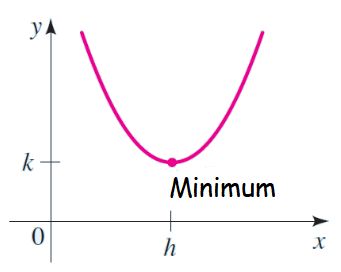



How To Find The Minimum Or Maximum Value Of A Function In Vertex Form




Review Of Vertex Form



The Parabola Shown Is Congruent To Y X 2 A What Are The Zeroes Of The Function B Write The Equation In Factored Form Quora



Vertex Form Chapter 4 Quad Relationships




Parabola Knowino




Quadratic Function




The Graph Of Y X2 6x 9 Is Shown Below What Is The Solution Set For Brainly Com




Vertical Shifts Of Quadratic Functions Ck 12 Foundation



Http Www Lakemills K12 Wi Us Faculty enzin Cms Files Event Attach 34 01 graphing quadratic equations Pdf



Axis Of Symmetry Of A Parabola



Untitled Document



Http Mrhudson Pbworks Com W File Fetch Quadratic functions booklet Pdf



Content Transformations Of The Parabola




Find The Coordinates Of A Point On The Parabola Y X 2 7x 2 Which Is Closest To The Straight Line Y 3x 3




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download




Resourceaholic Tricks And Tips 3 Quadratics



Consider A Parabola P That Is Congruent To Y X2 An Gauthmath



The Parabola Shown Is Congruent To Y X 2 A What Are The Zeroes Of The Function B Write The Equation In Factored Form Quora



School Ckseattle Org Documents 19 2 9 8 Equations Of Parabolas Pdf




Consider The Parabola Whose Equation Is Y X 2 4x And The Line Y 2x B Then Whichfollowing Is Are Correct




Axis Of Symmetry Of A Parabola




Using Properties Of Parabolas To Graph A Parabola Algebra And Geometry Help
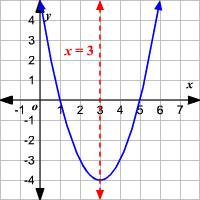



Axis Of Symmetry Of A Parabola



Graphing Quadratic Functions



L2d2ii Html



Blessedmotherteresa Typepad Com Files Graphingquadratics Day3 Pdf



Solution Can You Help Me With This Problem A Parabola Is Congruent To Y X 2 And Has X Intercepts 1 And 5 Determine The Coordinates Of The Vertex




Chapter 4 Quadratics 4 3 Using Technology To Investigate Transformations Ppt Download
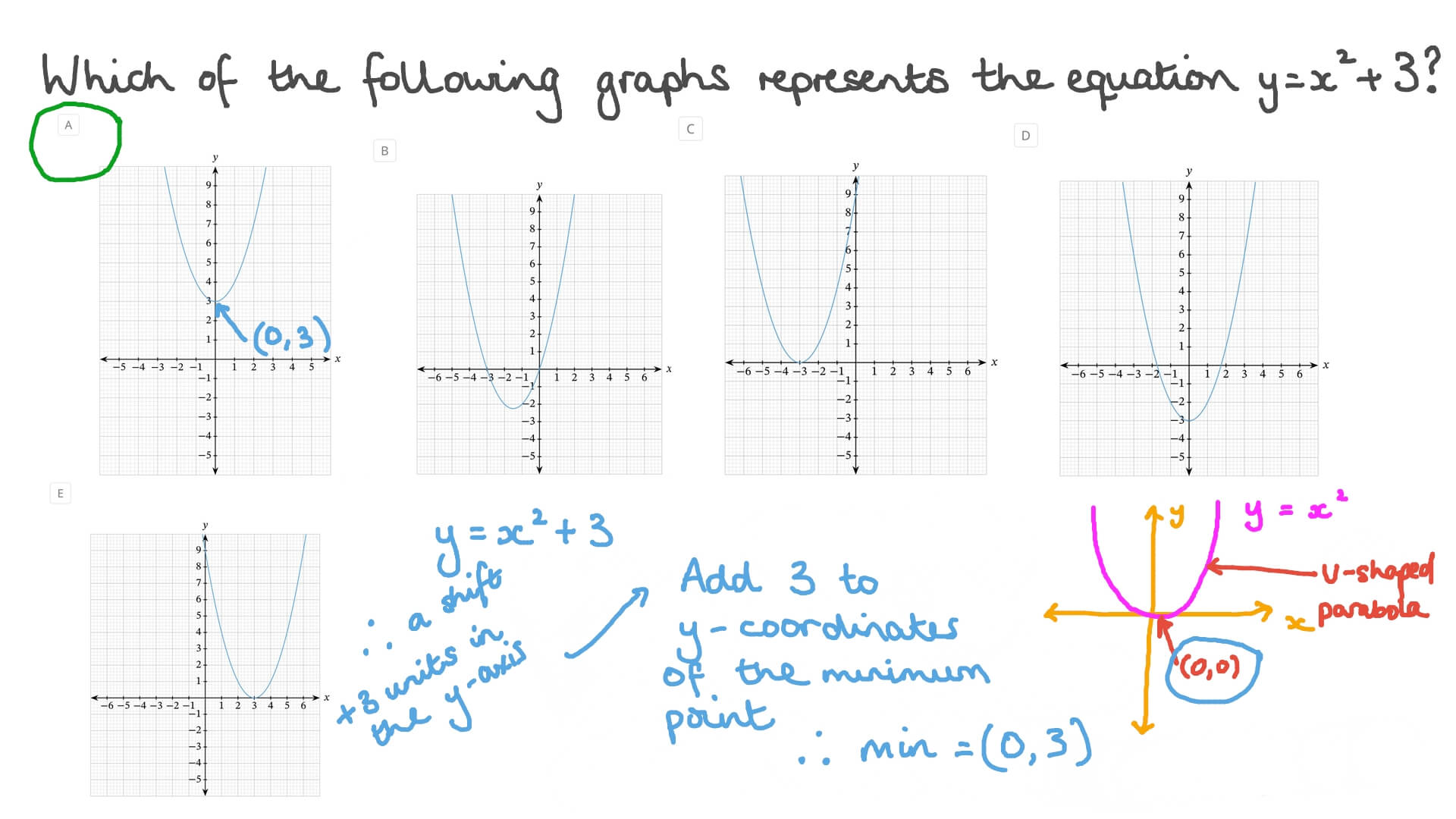



Question Video Identifying Graphs Of Quadratic Equations In Vertex Form Nagwa




Shifting Parabolas Video Khan Academy




Attributes Of Quadratic Flashcards Quizlet



2




Graphing Quadratic Functions Lesson Article Khan Academy
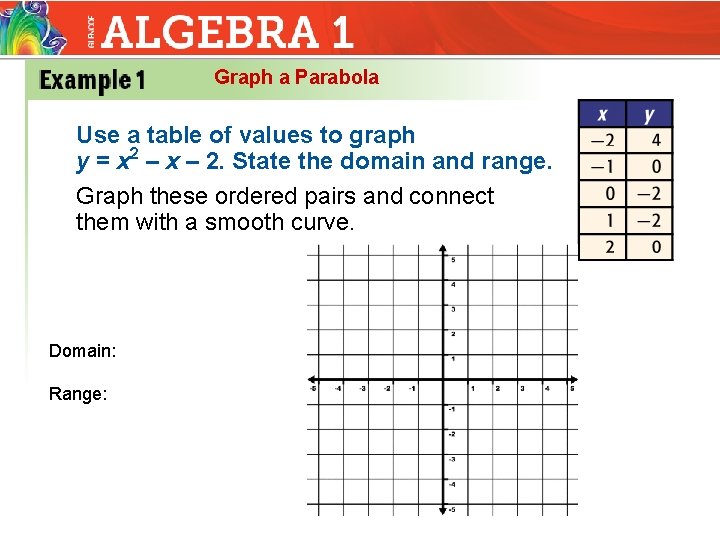



9 1 Identifying The Characteristics Of And Graphing



Fekggyhrwloe2m




Graphing Quadratic Functions




Write An Equation In Both Vertex Form And Standard Gauthmath
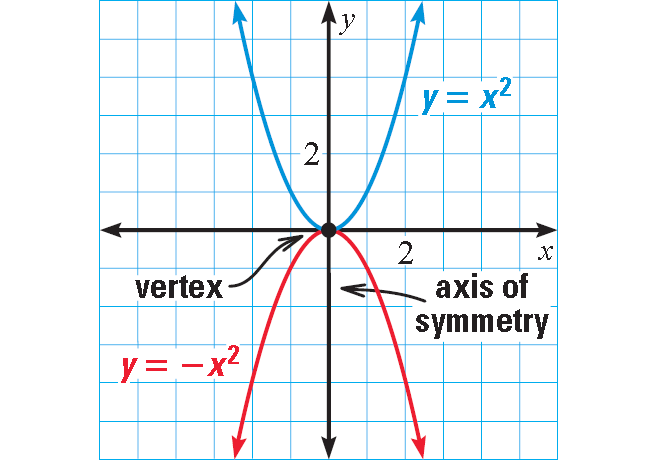



Graphing Quadratic Functions Parabola



What Is The Equation For A Parabola That Is Congruent To The Graph Of Y X Squared Opens Downward And Has Its Vertex At 3 1 Quora



The Parabola Shown Is Congruent To Y X 2 A What Are The Zeroes Of The Function B Write The Equation In Factored Form Quora




Quadratic Function



Math Spoken Here Classes Quadratic Equations 3



Content Transformations Of The Parabola



1



L2d2ii Html



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Quadratic Equation Congruent To Parabola Pass Through Point With Y Intercept As Another Curve Youtube



Exploration Of Parabolas




How To Find The Vertex Of A Quadratic Equation 10 Steps



Content Transformations Of The Parabola




Graphing Quadratic Functions Lesson Article Khan Academy
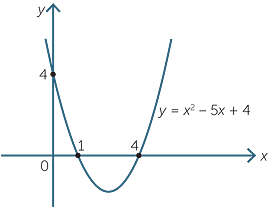



Quadratic Function



Www Engageny Org File Download Algebra Ii M1 Topic C Lesson 34 Teacher Pdf Token D04trqow
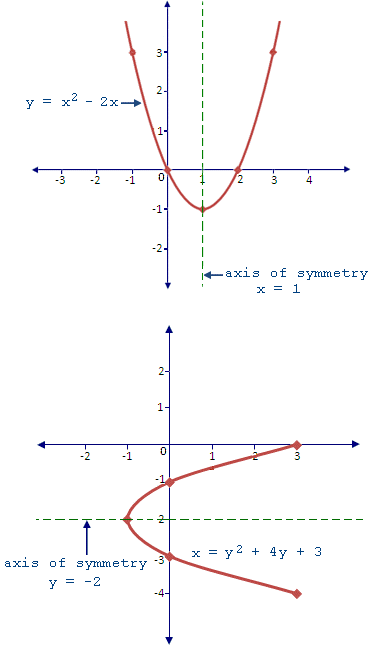



Axis Of Symmetry Of A Parabola



Math Quadratics Concept Map
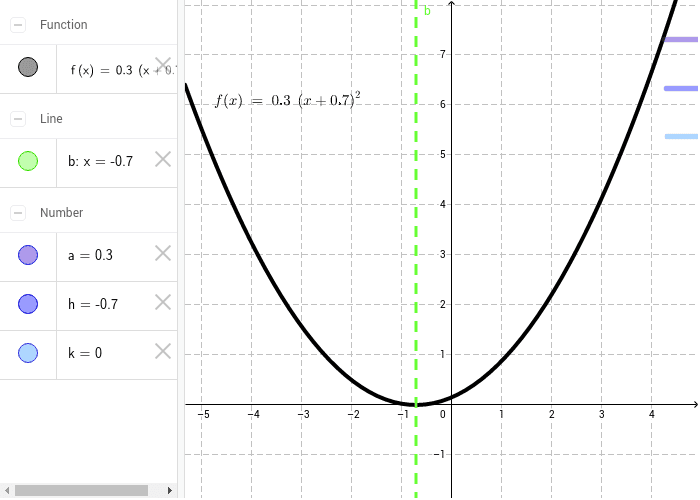



Transformations To The Graph Of Y X 2 Geogebra



Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 360 parabolas and properties packet Pdf



Exploration Of Parabolas




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com
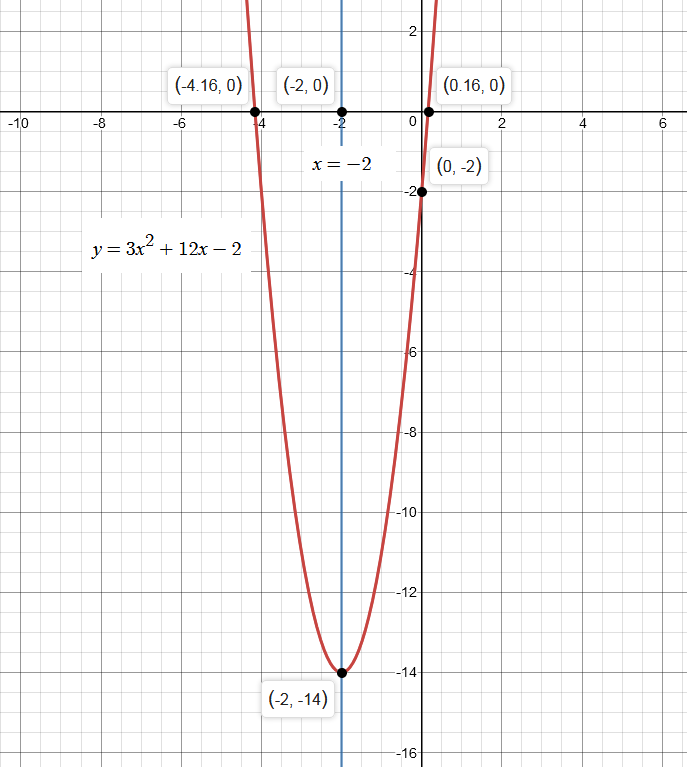



What Is The Axis Of Symmetry And Vertex For The Graph Y 3x 2 12x 2 Socratic



Http Blessedmotherteresa Typepad Com Files Graphingquadratics Day3 Pdf




Graphing Quadratic Functions Lesson Article Khan Academy




Find The Minimum Distance From The Parabola X Y 2 0 To The Point 0 3 Study Com




The Graph Of Y X 16 X Has Been Drawn What Lines Should Be Drawn On This Graph To Solve Following Brainly In



Review Of Vertex Form



How To Write The Vertex Of The Parabola Y X 2 8x 10 Quora



Congruent Parabolas Youtube




1 Point 17 Which Equation Describes A Parabola That Chegg Com




Algebra 1 Unit 7 Quadratic Functions Flashcards Quizlet




How To Find The Vertex Of A Quadratic Equation 10 Steps



1



Solution Find The Equation Of The Parabola With Vertex 4 4 The Parabola Opens Upwards And Is Congruent To Y 1 2x 2 Can You Please Help Me Thanks So Much In Advance
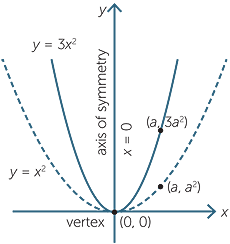



Quadratic Function
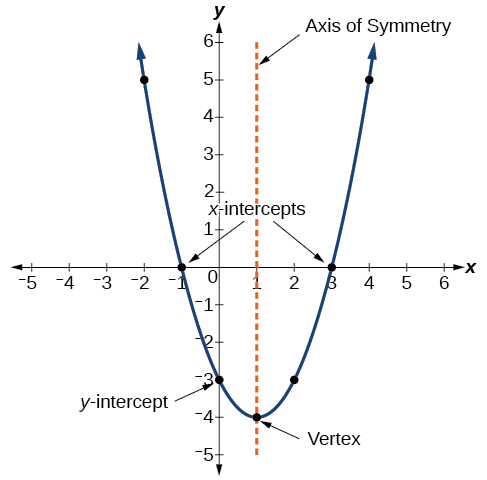



5 2 Quadratic Functions Mathematics Libretexts
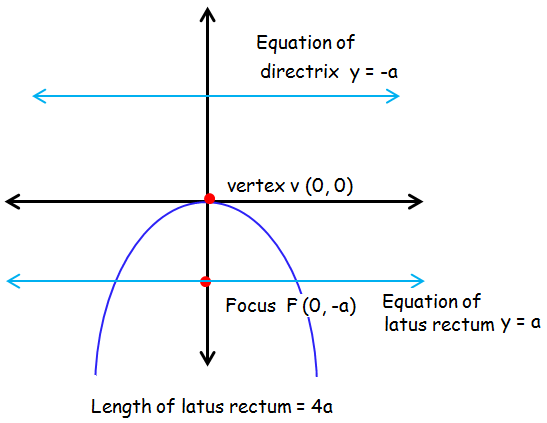



Parabola Formulas



0 件のコメント:
コメントを投稿